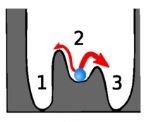
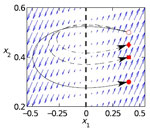
Asymmetry-induced synchronization in oscillator networks

It is generally assumed that individual entities are more likely to exhibit the same or similar behavior if they are equal to each other: think of lasers pulsing at the same frequency, animals using the same gait, agents reaching consensus. In a recent PRL paper we have shown that this assumption is in fact false in networks of interacting entities. Our central discovery is a network phenomenon we term “asymmetry-induced symmetry” (AIS), in which the state of the system can be symmetric only when the system itself is not symmetric. Using synchronization as a model process, we demonstrate that the state in which all nodes synchronize and exhibit identical dynamics (a state of maximum symmetry, as it remains unchanged after swapping any two nodes), such as when lasers pulse together, can only be realized when the nodes themselves are not identical. Asymmetry-induced symmetry can be seen as the converse of the well-studied phenomenon of symmetry breaking, where the state has less symmetry than the system. AIS has far-reaching implications for processes that involve converging to uniform states; in particular, it offers a mechanism for yet-to-be-explained convergent forms of pattern formation, in which an asymmetric structure develops into a symmetric one. AIS also has implications for consensus dynamics, where it gives rise to the scenario in which interacting agents only reach consensus when they are sufficiently different from each other. See also AIS Demo and AIS talk.

Main publications

T. Nishikawa and A.E. Motter,
Symmetric states requiring system asymmetry,
Phys. Rev. Lett. 117, 114101 (2016).
doi:10.1103/PhysRevLett.117.114101 - Synopsis
arXiv:1608.05419

Y. Zhang, T. Nishikawa, and A.E. Motter,
Asymmetry-induced synchronization in oscillator networks,
Phys. Rev. E 95, 062215 (2017).
doi:10.1103/PhysRevE.95.062215
arXiv:1705.07907

Y. Zhang and A.E. Motter,
Identical synchronization of nonidentical oscillators: When only birds of different feathers flock together,
Nonlinearity 31, R1 (2018).
doi:10.1088/1361-6544/aa8fe7
arXiv:1712.03245

J.D. Hart, Y. Zhang, R. Roy, and A.E. Motter,
Topological control of synchronization patterns: Trading symmetry for stability,
Phys. Rev. Lett. 122, 058301 (2019).
doi:10.1103/PhysRevLett.122.058301
arXiv:1902.03255

Z.G. Nicolaou, D. Eroglu, and A.E. Motter,
Multifaceted dynamics of Janus oscillator networks,
Phys. Rev. X 9, 011017 (2019).
doi:10.1103/PhysRevX.9.011017 - Synopsis - Animated summary
arXiv:1810.06576 - Explorable Iterative Interface

F. Molnar, T. Nishikawa, and A.E. Motter,
Network experiment demonstrates converse symmetry breaking,
Nature Physics 16, 351–356 (2020).
doi:10.1038/s41567-019-0742-y - Supplemental Material
arXiv:2009.05582 - Animated summary

Z.G. Nicolaou, M. Sebek, I.Z. Kiss, and A.E. Motter,
Coherent dynamics enhanced by uncorrelated noise,
Phys. Rev. Lett. 125, 094101 (2020).
doi:10.1103/PhysRevLett.125.094101
arXiv:2008.10654

F. Molnar, T. Nishikawa, and A.E. Motter,
Asymmetry underlies stability in power grids,
Nature Communications 12, 1457 (2021).
doi:10.1038/s41467-021-21290-5
arXiv:2103.10952

Y. Sugitani, Y. Zhang, and A.E. Motter,
Synchronizing Chaos with Imperfections,
Phys. Rev. Lett. 126, 164101 (2021).
doi:10.1103/PhysRevLett.126.164101
arXiv:2104.13376

Y. Zhang, J. L. Ocampo-Espindola, I. Z. Kiss, and A. E. Motter,
Random heterogeneity outperforms design in network synchronization,
Proc. Natl. Acad. Sci. USA 118(21), e2024299118, (2021).
doi.org/10.1073/pnas.2024299118
arXiv:2105.11476

Z.G. Nicolaou, D.J. Case, E.B. van der Wee, M.M. Driscoll, and A.E. Motter,
Heterogeneity-stabilized homogeneous states in driven media,
Nature Communications 12, 4486, (2021).
doi:10.1038/s41467-021-24459-0

J.L. Ocampo-Espindola, C. Bick, A.E. Motter, and I.Z. Kiss,
Frequency Synchronization Induced by Frequency Detuning,
Science Advances 11, eadu4114 (2025).
doi:10.1126/sciadv.adu4114
arXiv:2505.04714

A.E.D. Barioni, A.N. Montanari, and A.E. Motter,
Interpretable disorder-promoted synchronization and coherence in coupled laser networks,
Phys. Rev. Letters 135, 197401 (2025).
doi:10.1103/8qvk-hpwb
arXiv:2511.04749

A.N. Montanari, A.E.D. Barioni, C. Duan, and A.E. Motter,
Optimal flock formation induced by agent heterogeneity,
Nature Communications 16, 9626 (2025).
doi:10.1038/s41467-025-64233-0
arXiv:2504.12297v1

 

Small vulnerable sets determine large network cascades

The understanding of cascading failures in complex systems has been hindered by the lack of realistic large-scale modeling and analysis that can account for variable system conditions. Using the North American power grid, we identified, quantified, and analyzed the set of network components that are vulnerable to cascading failures under any out of multiple conditions. We show that the vulnerable set consists of a small but topologically central portion of the network and that large cascades are disproportionately more likely to be triggered by initial failures close to this set. These results elucidate aspects of the origins and causes of cascading failures relevant for grid design and operation and demonstrate vulnerability analysis methods that are applicable to a wider class of cascade-prone networks. For more information, please visit the original paper published in Science. Watch the animated summary of the paper here.

Main publications

A.E. Motter and Y.-C. Lai,
Cascade-based attacks on complex networks,
Phys. Rev. E 66, 065102 (2002).
Rapid Communications
doi:10.1103/PhysRevE.66.065102
arXiv:cond-mat/0301086

A.E. Motter,
Cascade control and defense in complex networks,
Phys. Rev. Lett. 93, 098701 (2004).
doi:10.1103/PhysRevLett.93.098701
arXiv:cond-mat/0401074

S. Sahasrabudhe and A.E. Motter,
Rescuing ecosystems from extinction cascades through compensatory perturbations,
Nature Communications 2, 170 (2011).
doi:10.1038/ncomms1163 - PDF - Supplementary Information
arXiv:1103.1653

A.E. Motter and Y. Yang,
The unfolding and control of network cascades,
Physics Today 70(1), 32 (2017).
doi:10.1063/PT.3.3426
arXiv:1701.00578

Y. Yang, T. Nishikawa, and A.E. Motter,
Vulnerability and cosusceptibility determine the size of network cascades,
Phys. Rev. Lett. 118, 048301 (2017).
doi:10.1103/PhysRevLett.118.048301 - Physics Story
arXiv:1701.08790

Y. Yang, T. Nishikawa, and A.E. Motter,
Small vulnerable sets determine large network cascades in power grids,
Science 358 (6365), eaan3184 (2017).
doi:10.1126/science.aan3184
arXiv:1804.06432

Y. Yang and A.E. Motter,
Cascading failures as continuous phase-space transitions,
Phys. Rev. Lett. 119, 248302 (2017).
doi:10.1103/PhysRevLett.119.248302 - COVER
arXiv:1712.04053

Network Control

See the talk Advances on the Control of Nonlinear Network Dynamics by Adilson E. Motter at the 2015 SIAM Conference on Applications of Dynamical Systems.

State observation and sensor selection for nonlinear networks

A large variety of dynamical systems, such as chemical and biomolecular systems, can be seen as networks of nonlinear entities. Prediction, control, and identification of such nonlinear networks require knowledge of the state of the system. However, network states are usually unknown, and only a fraction of the state variables are directly measurable. The observability problem concerns reconstructing the network state from this limited information. Here, we propose a general optimization-based approach for observing the states of nonlinear networks and for optimally selecting the observed variables. Our results reveal several fundamental limitations in network observability, such as the tradeoff between the fraction of observed variables and the observation length on one side, and the estimation error on the other side. We also show that, owing to the crucial role played by the dynamics, purely graph-theoretic observability approaches cannot provide conclusions about one's practical ability to estimate the states. We demonstrate the effectiveness of our methods by finding the key components in biological and combustion reaction networks from which we determine the full system state. Our results can lead to the design of novel sensing principles that can greatly advance prediction and control of the dynamics of such networks.

A. Haber, F. Molnar, and A.E. Motter,
State observation and sensor selection for nonlinear networks,
IEEE Trans. Control Netw. Syst. 5(2), 694 (2018).
doi:10.1109/TCNS.2017.2728201
arXiv:1706.05462

 

Control of stochastic and induced switching in biophysical networks

Noise caused by fluctuations at the molecular level is a fundamental part of intracellular processes. While the response of biological systems to noise has been studied extensively, there has been limited understanding of how to exploit it to induce a desired cell state. Here we present a scalable, quantitative method based on the Freidlin-Wentzell action to predict and control noise-induced switching between different states in genetic networks that, conveniently, can also control transitions between stable states in the absence of noise. We apply this methodology to models of cell differentiation and show how predicted manipulations of tunable factors can induce lineage changes, and further utilize it to identify new candidate strategies for cancer therapy in a cell death pathway model. This framework offers a systems approach to identifying the key factors for rationally manipulating biophysical dynamics, and should also find use in controlling other classes of noisy complex networks.

D.K. Wells, W.L. Kath, and A.E. Motter,
Control of stochastic and induced switching in biophysical networks,
Phys. Rev. X 5, 031036 (2015).
doi:10.1103/PhysRevX.5.031036 - Supplemental Material
arXiv:1509.03349

 

Optimal Least Action Control (OLAC) Algorithm

Daniel K. Wells, William L. Kath, and Adilson E. Motter

This work offers a ready-to-use code that can be applied to identify interventions to control transitions between attractors of large complex networks, both in the presence and in the absence of noise. The algorithm is highly scalable and applicable to systems with general nonlinear dynamics under rather general constraints on the feasible control interventions. To download the code and its description, please visit here.

 

Controllability transition and nonlocality in network control

A common goal in the control of a large network is to minimize the number of driver nodes or control inputs. Yet, the physical determination of control signals and the properties of the resulting control trajectories remain widely underexplored. Here we show that (i) numerical control fails in practice even for linear systems if the controllability Gramian is ill conditioned, which occurs frequently even when existing controllability criteria are satisfied unambiguously, (ii) the control trajectories are generally nonlocal in the phase space, and their lengths are strongly anti-correlated with the numerical success rate and number of control inputs, and (iii) numerical success rate increases abruptly from zero to nearly one as the number of control inputs is increased, a transformation we term numerical controllability transition. This reveals a trade-off between nonlocality of the control trajectory in the phase space and nonlocality of the control inputs in the network itself. The failure of numerical control cannot be overcome in general by merely increasing numerical precision — successful control requires instead increasing the number of control inputs beyond the numerical controllability transition.

J. Sun and A.E. Motter,
Controllability transition and nonlocality in network control,
Phys. Rev. Lett. 110, 208701 (2013).
doi:10.1103/PhysRevLett.110.208701
arXiv:1305.5848

 

Realistic control of network dynamics

The control of complex networks is of paramount importance in areas as diverse as ecosystem management, emergency response and cell reprogramming. A fundamental property of networks is that perturbations to one node can affect other nodes, potentially causing the entire system to change behaviour or fail. Here we show that it is possible to exploit the same principle to control network behaviour.

Our approach accounts for the nonlinear dynamics inherent to real systems, and allows bringing the system to a desired target state even when this state is not directly accessible due to constraints that limit the allowed interventions. Applications show that this framework permits reprogramming a network to a desired task, as well as rescuing networks from the brink of failure — which we illustrate through the mitigation of cascading failures in a power-grid network and the identification of potential drug targets in a signalling network of human cancer.

S.P. Cornelius, W.L. Kath, and A.E. Motter,
Realistic control of network dynamics,
Nature Communications 4, 1942 (2013).
doi:10.1038/ncomms2939 - PDF - Supplementary Information - Movie
arXiv:1307.0015v1

NECO - A scalable algorithm for NEtwork COntrol

We present an algorithm for the control of complex networks and other nonlinear, high-dimensional dynamical systems. The computational approach is based on the recently-introduced concept of compensatory perturbations — intentional alterations to the state of a complex system that can drive it to a desired target state even when there are constraints on the perturbations that forbid reaching the target state directly. Included here is ready-to-use software that can be applied to identify eligible control interventions in a general system described by coupled ordinary differential equations, whose specific form can be specified by the user. The algorithm is highly scalable, with the computational cost scaling as the number of dynamical variables to the power 2.5.

S.P. Cornelius and A.E. Motter,
NECO - A scalable algorithm for NEtwork COntrol,
Protocol Exchange (2013), doi:10.1038/protex.2013.063.
doi:10.1038/protex.2013.063 - Source Codes
arXiv:1307.2582

 

Other publications

A.E. Motter,
Cascade control and defense in complex networks,
Phys. Rev. Lett. 93, 098701 (2004).
doi:10.1103/PhysRevLett.93.098701
arXiv:cond-mat/0401074

A.E. Motter, N. Gulbahce, E. Almaas, and A.-L. Barabási,
Predicting synthetic rescues in metabolic networks,
Molecular Systems Biology 4, 168 (2008).
doi:10.1038/msb.2008.1 - Supplementary Information - EMBO and Nature Publishing Group
arXiv:0803.0962

D.-H. Kim and A.E. Motter,
Slave nodes and the controllability of metabolic networks,
New J. Phys. 11, 113047 (2009).
doi:10.1088/1367-2630/11/11/113047 - Supplementary Information
arXiv:0911.5518

A.E. Motter,
Improved network performance via antagonism: From synthetic rescues to multi-drug combinations,
BioEssays 32, 236 (2010) - Problems and Paradigms.
doi:10.1002/bies.200900128 - Online Open
arXiv:1003.3391

S. Sahasrabudhe and A.E. Motter,
Rescuing ecosystems from extinction cascades through compensatory perturbations,
Nature Communications 2, 170 (2011).
doi:10.1038/ncomms1163 - PDF - Supplementary Information
arXiv:1103.1653

Y. Yang, J. Wang, and A.E. Motter,
Network observability transitions,
Phys. Rev. Lett. 109, 258701 (2012).
doi:10.1103/PhysRevLett.109.258701 - Supplementary Information
arXiv:1301.5916

A.E. Motter, S.A. Myers, M. Anghel, and T. Nishikawa,
Spontaneous synchrony in power-grid networks,
Nature Physics 9, 191 (2013).
doi:10.1038/nphys2535 - Supplementary Information
arXiv:1302.1914

A.E. Motter,
Networkcontrology,
Chaos 25, 097621 (2015).
doi:10.1063/1.4931570
arXiv:1510.08320

C. Duan, P. Chakraborty, T. Nishikawa, and A.E. Motter,
Hierarchical power flow control in smart grids: Enhancing rotor angle and frequency stability with demand-side flexibility,
IEEE Trans. Control Netw. Syst. 8 (3), 1046 (2021).
doi:10.1109/TCNS.2021.3070665
arXiv:2108.05898

A.N. Montanari, C. Duan, L.A. Aguirre, and A.E. Motter,
Functional observability and target state estimation in large-scale networks,
Proc. Natl. Acad. Sci. USA 119(1), e2113750119 (2022).
doi:10.1073/pnas.2113750119
arXiv:2201.07256

C. Duan, T. Nishikawa, and A.E. Motter,
Prevalence and scalable control of localized networks,
Proc. Natl. Acad. Sci. USA 119(32), e2122566119 (2022).
doi.org/10.1073/pnas.2122566119 - Supplemental Material
arxiv:2208.05980

A. Haber, F. Molnar, and A.E. Motter,
Global network control from local information,
Chaos 34, 123166 (2024).
doi:10.1063/5.0239177
arXiv:2501.03331

A.N. Montanari, C. Duan, and A.E. Motter,
On the Popov-Belevitch-Hautus tests for functional observability and output controllability,
Automatica 174, 112122 (2025).
doi:10.1016/j.automatica.2025.112122
arXiv:2402.03245

Y. Wang, A.N. Montanari, and A.E. Motter,
Distributed Lyapunov Functions for Nonlinear Networks,
IEEE Control Systems Letters 9, 486 (2025).
doi:10.1109/LCSYS.2025.3573881
arXiv:2506.20728

A.N. Montanari, C. Duan, and A.E. Motter,
Duality between controllability and observability for target control and estimation in networks,
IEEE Transactions on Automatic Control 70,5584 (2025).
doi:10.1109/TAC.2025.3552001
arXiv:2401.16372

Mechanical metamaterials with negative compressibility transitions

When tensioned, ordinary materials expand along the direction of the applied force. In our recent Nature Materials paper, we explore network concepts to design metamaterials exhibiting negative compressibility transitions, during which a material undergoes contraction when tensioned (or expansion when pressured). Continuous contraction of a material in the same direction of an applied tension is inherently unstable. The conceptually similar effect we demonstrate can be achieved, however, through destabilizations of (meta)stable equilibria of the constituents. These destabilizations give rise to a stress-induced solid-solid phase transition associated with a twisted hysteresis curve for the stress-strain relationship. We suggest that the proposed materials could be useful for the design of actuators, force amplifiers, micromechanical controls, and protective devices.

• Movie: Simulated response of the material to uniform, diagonal, pinched, and splayed stress profiles.

Main publications

Z.G. Nicolaou and A.E. Motter,
Mechanical metamaterials with negative compressibility transitions,
Nature Materials 11, 608 (2012).
doi:10.1038/nmat3331 - Supplementary Information - Movie - Nontechnical Overview Article
arXiv:1207.2185

Z.G. Nicolaou and A.E. Motter,
Longitudinal inverted compressibility in super-strained metamaterials,
J. Stat. Phys. 151(6), 1162 (2013).
doi:10.1007/s10955-013-0742-8
arXiv:1304.0787

Z.G. Nicolaou, F. Jiang, and A.E. Motter,
Metamaterials with negative compressibility highlight evolving interpretations and opportunities,
Nature Communications 15, 8573 (2024).
doi:10.1038/s41467-024-52853-x